Doob's martingale inequality
In mathematics, Doob's martingale inequality is a result in the study of stochastic processes. It gives a bound on the probability that a stochastic process exceeds any given value over a given interval of time. As the name suggests, the result is usually given in the case that the process is a non-negative martingale, but the result is also valid for non-negative submartingales.
The inequality is due to the American mathematician Joseph Leo Doob.
Contents |
Statement of the inequality
Let X be a submartingale taking non-negative real values, either in discrete or continuous time. That is, for all times s and t with s < t,
(For a continuous-time submartingale, assume further that the process is càdlàg.) Then, for any constant C > 0 and p ≥ 1,
In the above, as is conventional, P denotes the probability measure on the sample space Ω of the stochastic process
and E denotes the expected value with respect to the probability measure P, i.e. the integral
in the sense of Lebesgue integration. 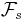 denotes the σ-algebra generated by all the random variables Xi with i ≤ s; the collection of such σ-algebras forms a filtration of the probability space.
denotes the σ-algebra generated by all the random variables Xi with i ≤ s; the collection of such σ-algebras forms a filtration of the probability space.
Further inequalities
There are further (sub)martingale inequalities also due to Doob. With the same assumptions on X as above, let
and for p ≥ 1 let
In this notation, Doob's inequality as stated above reads
The following inequalities also hold: for p = 1,
and, for p > 1,
Related inequalities
Doob's inequality for discrete-time martingales implies Kolmogorov's inequality: if X1, X2, ... is a sequence of real-valued independent random variables, each with mean zero, it is clear that
so Mn = X1 + ... + Xn is a martingale. Note that Jensen's inequality implies that 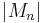 is a nonnegative submartingale if
is a nonnegative submartingale if 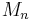 is a martingale. Hence, taking p = 2 in Doob's martingale inequality,
is a martingale. Hence, taking p = 2 in Doob's martingale inequality,
which is precisely the statement of Kolmogorov's inequality.
Application: Brownian motion
Let B denote canonical one-dimensional Brownian motion. Then
The proof is just as follows: since the exponential function is monotonically increasing, for any non-negative λ,
By Doob's inequality, and since the exponential of Brownian motion is a positive submartingale,
Since the left-hand side does not depend on λ, choose λ to minimize the right-hand side: λ = C / T gives the desired inequality.
References
- Revuz, Daniel and Yor, Marc (1999). Continuous martingales and Brownian motion (Third ed.). Berlin: Springer. ISBN 3-540-64325-7. (Theorem II.1.7)
- Shiryaev, Albert N. (2001), "Martingale", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=M/m062570
![\mathbf{E} \big[ X_{t} \big| \mathcal{F}_{s} \big] \geq X_{s}.](/2012-wikipedia_en_all_nopic_01_2012/I/2bf3f76f7fa74657a59010000d4f7ca5.png)
![\mathbf{P} \left[ \sup_{0 \leq t \leq T} X_{t} \geq C \right] \leq \frac{\mathbf{E} \big[ X_{T}^{p} \big]}{C^{p}}.](/2012-wikipedia_en_all_nopic_01_2012/I/cacbd07af37c052b5cf019b67647646f.png)
![X�: [0, T] \times \Omega \to [0, %2B \infty)](/2012-wikipedia_en_all_nopic_01_2012/I/1720de411f284a93044fb62a691d3054.png)
![\mathbf{E} \big[ X_{T} \big] = \int_{\Omega} X_{T} (\omega) \, \mathrm{d} \mathbf{P} (\omega)](/2012-wikipedia_en_all_nopic_01_2012/I/2106ec64f3188f0975c76576d89c2621.png)
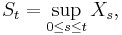
![\| X_{t} \|_{p} = \| X_{t} \|_{L^{p} (\Omega, \mathcal{F}, \mathbf{P})} = \left( \mathbf{E} \big[ | X_{t} |^{p} \big] \right)^{1 / p}.](/2012-wikipedia_en_all_nopic_01_2012/I/66d927db35b6c414e4b4ecb540a1d949.png)
![\mathbf{P} \left[ S_{T} \geq C \right] \leq \frac{\| X_{T} \|_{p}^{p}}{C^{p}}.](/2012-wikipedia_en_all_nopic_01_2012/I/1b3db414d7ee777774354d51f2ec7445.png)
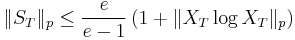
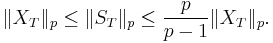
![\mathbf{E} \big[ X_{1} %2B \dots %2B X_{n} %2B X_{n %2B 1} \big| X_{1}, \dots, X_{n} \big]](/2012-wikipedia_en_all_nopic_01_2012/I/b04fd32d207e5cd3083957ab086cab17.png)
![= X_{1} %2B \dots %2B X_{n} %2B \mathbf{E} \big[ X_{n %2B 1} \big| X_{1}, \dots, X_{n} \big]](/2012-wikipedia_en_all_nopic_01_2012/I/3ff042be45e9fbf9b3abd88bfa118952.png)

![\mathbf{P} \left[ \max_{1 \leq i \leq n} \big| M_{i} \big| \geq \lambda \right] \leq \frac{\mathbf{E} \big[ M_{n}^{2} \big]}{\lambda^{2}},](/2012-wikipedia_en_all_nopic_01_2012/I/438c845595618dbf64c42cd0f63d8254.png)
![\mathbf{P} \left[ \sup_{0 \leq t \leq T} B_{t} \geq C \right] \leq \exp \left( - \frac{C^2}{2 T} \right).](/2012-wikipedia_en_all_nopic_01_2012/I/4df4042444a5cd2a823d81b6953d89bf.png)
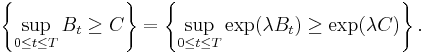
![\begin{align}
& \mathbf{P} \left[ \sup_{0 \leq t \leq T} B_{t} \geq C \right] \\
& = \mathbf{P} \left[ \sup_{0 \leq t \leq T} \exp ( \lambda B_{t} ) \geq \exp ( \lambda C ) \right] \\
& \leq \frac{\mathbf{E} \big[ \exp (\lambda B_{T}) \big]}{\exp (\lambda C))} \\
& = \exp \left( \frac{\lambda^{2} T}{2} - \lambda C \right) \mbox{ since } \mathbf{E} \big[ \exp (\lambda B_{t}) \big] = \exp \left( \frac{\lambda^{2} t}{2} \right).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/bd4f7038c9237b3c70d738518637525f.png)